🔥udemy cyber monday ,課程最低價 NT 330 元起
課程說明
世界上所有電腦科學、資訊工程、資料管理主修的學生,都在學習電腦科學!
隨著電腦科學的飛速發展,離散數學的重要性則日益彰顯。它為許多資訊學課程提供了數學基礎,包括資料結構、演算法、資料庫理論、形式語言與作業系統等。如果沒有離散數學的相關數學基礎,學生在學習上述課程中,便會遇到較多的困難。
離散數學包含邏輯、證明、遞迴關係、演算法、數論與密碼學、演算法分析、圖形理論、路徑選擇、機率、排列組合、以及其他重要的程式開發演算法! 這堂課會深入淺出探討這些概念,並且用 Python 或JavaScript (二擇一) 來做演算法練習!
在學習這堂課之後,你將能夠:
1. 學會推導邏輯與驗證程式碼邏輯正確性。
2. 用邏輯來證明數學理論,做為資料科學的的重要演算法基礎。
3. 了解遞迴演算法與遞迴數列關係,準備好你自己回答Coding Interview面試中的問題。
4. 能夠用程式碼表現出「歐幾里得演算法」、「歐拉函數」、「河內塔問題」、「最小公倍數演算法」、「斐波那契數列」、「線性遞迴關係式」、還有其他重要的演算法!
5. 學習數論與集合理論,作為學習質數與密碼學的重要演算法基礎。
6. 學習基本圖形理論,判斷圖形資料結構。
7. 學會圖形演算法,例如「Floyd-Warshall 演算法 (Dynamic Programming)」、「Dijkstra’s Algorithm」、「Depth First Traversal」、「Breadth First Traversal」。
8. 計算離散架構中的排列組合,並了解機率計算方法。
9. 能夠判斷與分析不同的演算法。
10. 用 Python 或 JavaScript 來實現離散數學的演算法與架構!
https://softnshare.com/discrete-math-with-python-and-javascript/
同時也有52部Youtube影片,追蹤數超過4萬的網紅吳老師教學部落格,也在其Youtube影片中提到,Python基礎程式語言應用證照班第10次上課 01_重點回顧與證照508最大公因數 02_證照508最大公因數解答 03_證照510費氏數列題目說明 04_證照510費氏數列無函式解答 05_證照510費氏數列加上函式解答 06_證照602撲克牌總和解答一 07_證照602撲克牌總和解答二改用串...
「遞迴數列解法」的推薦目錄:
- 關於遞迴數列解法 在 軟體開發學習資訊分享 Facebook 的最佳解答
- 關於遞迴數列解法 在 光引擎 Facebook 的最讚貼文
- 關於遞迴數列解法 在 Kamini卡蜜尼 Facebook 的精選貼文
- 關於遞迴數列解法 在 吳老師教學部落格 Youtube 的精選貼文
- 關於遞迴數列解法 在 吳老師教學部落格 Youtube 的精選貼文
- 關於遞迴數列解法 在 吳老師教學部落格 Youtube 的最讚貼文
- 關於遞迴數列解法 在 [分享] 遞迴數列自創解法- 看板tutor - 批踢踢實業坊 的評價
- 關於遞迴數列解法 在 高中數學討論區| 各位先進、各位同學們大家午安 ... 的評價
- 關於遞迴數列解法 在 混合型遞迴及其範例 - YouTube 線上影音下載 的評價
- 關於遞迴數列解法 在 費式數列 的評價
- 關於遞迴數列解法 在 Re: [中學] 遞迴數列- math | PTT學習區 的評價
遞迴數列解法 在 光引擎 Facebook 的最讚貼文
Q.E.D.
quod erat demonstrandum 故得證之意,
宣示定理真實性的建立。
這是一首歌頌知識與真理的歌曲。
步入社會後,就會開始懷念起學生時代單純的美好。在純粹知識的世界裡,一切如此分明。長大後的世界,是非界線變得模糊,令人不知所措。儘管如此,我們依舊努力用著自己的方式,追尋著那個,絕對純粹的世界。
-----------------------------------------------------------
3.1415927
16384次艱辛 (註1)
追尋與真理最近距離
轉角遇見費布納西 (註2)
鸚鵡螺的曲線曼妙美麗
樹葉一片片排列整齊
畢達哥拉斯和商高先生
都發現勾股弦中的秘密 (註3)
引領千年後費瑪最後定理 (註4)
懷爾斯的熱情與堅定不移
解開懸宕三百年的世紀謎題
127.0.0.1 (註5)
最美好的秘密基地
二進位言語
改變世界的超能力
沒有終止條件的遞迴函式 (註6)
不斷呼喊自己 不到終點永不放棄
一次一次一次證明 都更接近真理
零是零 一是一 這世界黑白分明
不同不同不同 不同於模糊難解的人心
這浩瀚宇宙是如此美麗
一次一次一次 接近真理
零是零 一是一 絕對的純粹
不同不同不同 不同於模糊難解的人心
這浩瀚宇宙是如此美麗
-----------------------------------------------
(註1)古代數學家用正多邊形的面積來逼近圓面積,原理簡單,但計算時要不斷開平方,過程非常繁複。南北朝的祖沖之算到16384邊,而得知圓周率介於3.1415926與3.1415927之間。
(註2) 費布納西(Fibonacci)數列:1,1,2,3,5,8,13,21,34,55... 費布納西於西元1202年提出,在葉序問題、最佳化理論、結晶結構等領域都有直接應用。
(註3)畢氏定理,又稱商高定理或勾股弦定理,a2 + b2 = c2。
(註4)費瑪最後定理,源於畢氏定理,17世紀的數學怪傑費瑪在書頁空白處寫下:「xn + yn = zn,當n大於2時沒有整數解。我已為這個命題找到一個非常巧妙的證明,然而這裡狹窄的篇幅不足以讓我寫下。」如此簡短的敘述,卻成為數學史上最深奧的謎團。一直到二十世紀,才由安德魯懷爾斯(Andrew Wiles)破解。
(註5) 127.0.0.1 = localhost = home
(註6)遞迴(recursion),是「函式(function)不斷呼叫自身」的一種程式撰寫法。而為了防止程式無窮盡的遞迴下去,必須為所寫出來的遞迴函式設定一個終止條件(termination condition)。
http://tw.streetvoice.com/music/lightengine/song/188032/
遞迴數列解法 在 Kamini卡蜜尼 Facebook 的精選貼文
比例始終如一,1比1.618,周而復始地出現既定的模式,隱匿於眾目睽睽之下,只須摸清門道,就能解開其中奧妙,多數人看來雜亂無章的事物,其實暗藏玄機,銀河星系、莊家植被、海洋貝類,行為模式皆有跡可循,可是僅有少數人能看清其中的關聯,69億1千9百37萬7千人住在這個小星球上,這是個關於其中某些人的故事。在中國古代,有個關於命運紅線的神話,據說眾神在每個人的腳踝上,繫有一根紅線,並將另一端繫在註定與我們命運交會的人身上,這根紅線,時而繃緊時而纏結,但卻永不斷裂,這一切全由數學概率注定,而我的職責就是追蹤這些數字,為找尋彼此,渴求生命交會的雙方,牽線搭橋。比例始終如一,1比1.618周而復始地出現其中模式,既定的數學原理,隱匿于眾目睽睽之下,只須摸清門道,就能解開其中奧妙,我們這個世界上有6919377000個人,只有少數人能看出其中的聯繫,今天我們會發出超過三千億封的郵件,190億條短信,但我們仍然感覺孤獨,平均每人對7.4個人說2250個字,這些字是否會傷害他人或是治癒他人?在中國古代,有個關於命運紅線的神話,據說眾神在每個人的腳踝上繫有一根紅線,並將另一端繫在註定與我們命運交會的人身上,這根紅線,時而繃緊時而纏結,但是它絕對不會斷裂
、 平均每人會對7.4個人,說2250個字,發出超過3000億封的郵件,190億條短信,構成各種模式和比例的交織 甚是壯觀,以數學形式表現,這些模式隱匿於眾目睽睽之下,只須摸清門道 方解其中奧妙,可只有少數人能看清其中的關聯,這一切全由數學概率註定,而我的職責就是追蹤這些數字為,找尋彼此,渴求生命交匯的雙方,牽線搭橋。70億人,擠在一個浩瀚宇宙中的小星球上,各自存在這個矛盾,是我們脆弱生命中的最大謎團,也許是彼此寂寞的存在於宇宙中,才把我們聯繫在一起,也許正是宇宙中各自的存在創造了"量子糾纏",糾纏你糾纏我,糾纏著我們。如果這是真的,那我們生存的這個世界中,一切皆有可能。
、 熱帶雨林中,生活著三百萬種動物,其中一種 叫做紅火蟻,具強烈攻擊性的螞蟻 被其叮咬後會產生如火灼燒般疼痛感,其後會出現如灼傷般的水泡,生存在地下 常年經受著,被山洪暴發消滅的威脅,大自然才不在意,如果一個物種想要存活下去,它就要證明自己存在的價值。當洪水來臨,紅火蟻們緊緊團結在一起,將自身組合成一個木筏,浮在水面,直到洪水退去,有時甚至要漂流幾個月,這些物種是如何得知這類方法的呢?憑直覺?還是不斷嘗試摸索?會不會有一隻紅火蟻,被洪水沖走,然後撞上了另一隻螞蟻?結果發現它們倆合在一起可以漂浮,如果你就是那個,知道應對措施的人,卻無法言表呢?你怎麼讓別人明白?你怎麼求助?人類並不是地球上最強大的物種,我們不是最敏捷的,或許甚至不是最聰明的。我們擁有的一個優勢,就是我們的合作能力,互相幫助,脫離困境。我們在彼此之間認清自己,激發出憐憫、英勇還有愛,這些本能,那些東西,使我們變得更加強大更加敏捷更加聰明,所以我們存活了下來,這就是我們想存活下去的原因。
、 第一根橫渡大西洋的電報電纜,由340,500英里長的銅絲鐵絲構成,在海底延伸2,876.95海浬,當這些電線就位,人們就能利用電脈衝和通信密碼,向世界另一端的人,自由地傳遞資訊。人類天生就有與人分享想法,和渴望被傾聽的欲望,這都源自於我們對集體生活的需要,所以我們不停地發送訊息和信號,同時也向別人尋求它們。我們總在等待訊息,希望與人有所連接。不管通信科技多麼發達,都不會有任何發明,比人類的聲音更有效,當人類的聲音出現,我們本能地會去傾聽,並希望能夠理解,即便說話的人只是在搜尋合適的詞語,即便我們所聽到的只有嘶吼、呼喊或吟唱,由於人類聲音的共振,不同於世間萬物,所以我們能夠在整個交響樂團的伴奏聲中,聽到歌者的聲音,不論是什麼樂器伴奏,我們總能聽見歌者的聲音。
、 今天會有490,000個嬰兒出生,它們每個獨一無二,成為更強大的人類鏈上的一環,就在臍帶被剪斷的那一刻,他們成為了個體,有各自的希望、夢想和心願,其實我們每個人由很多系統構成,這些系統依次由六十萬億細胞,和細胞中無數的蛋白質、DNA、細胞器構成,看似獨立的個體,實際上卻是一個網狀系統,我們每個人其實都是一個有生命,會呼吸的族群,但又不僅僅僅如此,為什麼會這樣呢?每一個你懷抱的希望,心存的夢想,實現的心願,都有深遠的影響,深遠到你無法想像,至少從我的角度看,是這樣。連接著我們的那條線,是不受時間和地域限制的,對個人來講,看起來像是扭曲命運的單一事件,而從另一個角度看來,不過是其中的一條線被拉緊而已,世事皆有定數,即使這些線看似磨損到無法修補,卻從沒斷過,完全不會斷,但有時候最重要的連結,就是此時此刻。
、 89度15分50.8秒,是此刻北極星的位置,北方的星星,從其它星球看,只是眾多星球中的一顆,可是在地球上,它格外重要,固定不動,就像船錨,不論你身處北半球的任何地方,看見北極星,就是面向北方,你知道自己的位置。但仍有很多方式會讓我們迷失,例如做出的選擇、壓垮我們的事件、甚至在我們的思緒之中,這時候,什麼東西可以作為船錨?什麼燈塔可以指引我們從黑暗走向光明?可能是其他人嗎?生活中多多少少打動我們的人,和北極星不同的是,這些人帶給我們的光明永不泯滅。
、 數字在改變之前,一直是恒定的。我們對於結果的無能為力,就是重要的均衡器,它讓世間變得公平。計算機產生著隨機數字,企圖從機率中找到意義無盡的數列,毫無規律可循。面對全球性的災難事件、海嘯、地震,9/11恐怖攻擊,這些隨機數字突然變得不再隨機,一旦人類的集體意識同步,數字也變得同步,科學無法解釋此現象,但宗教可以,那就是禱告,禱告是一種集體訴求,人們的一致行動,是共同的希望,數字在改變之前,一直是恒定的。面對全球性的災難事件,人類的集體意識同步,隨機產生的數列 也變得同步,科學解釋不了這一現象 但是宗教可以,稱之為禱告,禱告是一種集體訴求,建立起人們的一致行動,共同的願望、恐懼釋放、一個被寬恕的生命。數字發生變化之前,一直是恒定的,在悲傷的時候,集體狂歡的時刻,這些短暫的瞬間,是人們唯一共有的情感經驗,讓世界不那麼混亂無序,也許只是巧合,也許那就是我們禱告的答案。
、 兩點之間線段最短,如果那條路線被阻擋了,會怎樣?當河底沉積,阻礙了河水流向,水流便會改變方向,不再直線流動,而是曲折前行。烏鴉眼中蜿蜒的河流,正是河水從源頭流向河口的最有效路線,自然本身形成了迂回路線。如果兩點註定相遇,但直接相連又無法實現,宇宙總會找到其它辦法。如果兩點註定有交集,那麼宇宙總能使它們相連,即便所有希望似乎會落空,既定的鏈結也不會被打破,這些鏈結決定了我們的身份,以及我們的將來,穿越空間,穿越時間,沿著我們無法預知的條條道路,冥冥之中自有安排。
、 半音音階由十二個音調組成,按照時間順序排列這十二個簡單的音調,就能組合出千變萬化的音樂,和諧與不和諧,緊張與舒緩,都可以通過音調的數學定比,來加以描述。我們能把所有的比例轉化成聲音嗎?我們能聽見蒼穹之音,如同宇宙一般遼闊,一般有力,但也如同單一石頭般靜謐,如同人心令人陶醉,對某些人來說,音樂將他的靈魂昇華到無與倫比的美麗,有些人能單純聽見數字中的美麗。地球在運轉的過程中,發出7.8赫茲的頻率或是音符,但是這個頻率,由於目前還未知的原因,會發出細微的變化,有些人假設這是由於太陽黑子或是大氣中的電流擾動,但是或許原因比這更簡單,也許這個星球聲音的變化,是受到地表生活著的七十億生命的影響,每一個生命都創作著自己的音樂,添加著自己的和諧音符。
、 對稱是宇宙的語言,以數學的形式表達出來,字母就是三角形、圓形以及其它幾何圖形,沒有這些圖形,人類絲毫無法理解宇宙的語言,但我們當中,有人懂得這些語言,他們能準確地看清其中的模式,看清這星羅棋布的世界,那些幾何圖形互相呼應,周而復始,當你懂得這種語言,跟隨邏輯的腳步,你便能預測未來,你只需堅信命運指明的方向。蜂巢中的單個小窩,儘管拼圖的每一塊,都不可能真正交錯,但它們都組成了同樣重要的馬賽克,如同牆磚,每一塊磚都讓整座牆更加堅挺,抽走一塊,整座墻都會分崩離析,儘管我們可能尚未察覺牆體的完整性,每天都在接受考驗,但牆屹立不倒,這是因為每個人合力支撐。
、 1992年,一個集裝箱從貨船上墜入大海,當時該船正從中國駛往美國,兩萬九千隻橡皮小鴨散落太平洋,十個月後,人們首先在阿拉斯加海岸發現了被沖上岸的橡皮小鴨,此後,這些橡皮小鴨相繼出現在夏威夷、南美洲、澳洲,甚至緩緩漂到北極,凍在冰塊裡。還有兩千隻橡皮小鴨被困在北太平洋環流,一個由日本海域、阿拉斯加海域、北太平洋西部海域和阿留申群島海域洋流運轉構成的漩渦。被捲入漩渦的物品,通常會永遠留在裡面,註定以同樣的路線漂流,永遠在同一片海面打轉,但也有特例,漂流的路線也會變化,例如發生天氣變化、海上風暴,或是碰上鯨群,橡皮小鴨散落太平洋,已是二十年前的事,但這些小鴨還是會出現在世界各地的海灘,而同時漩渦中的橡皮小鴨數量有所減少,也意味著,掙脫束縛不是不可能,就算多年在同一片海面打轉,也總有到達海岸的可能。捲入漩渦的事物通常會留在漩渦中,註定沿著相同的軌道旋轉,永遠在同一水流中循環往復,但也可能並非一如既往,它們的軌道因氣候變化而被改變,大海上的暴風雨,可能會遇到一群鯨魚,可能因此掙脫束縛,即便在水中迴旋了多年,也可能設法打住。
、 一年有三千一百五十三萬秒,一秒又有一千毫秒、一百萬微秒、十億奈秒,連接著奈秒和年的常數就是變化。宇宙中,從原子到星系都處在永恆的變化之中,但我們人類不喜歡變化,我們與之抗爭,我們畏懼變化,所以我們創造了靜止的幻象,我們希望當下的這個世界靜止,,但這恰恰符合一個著名的悖論,你以為抓住了"現在"的那一瞬間,那個"現在"已經過去了,我們依賴照相,但生活是移動的照片,即便是微不足道的奈秒,也與之前不同。時間強迫我們成長,去適應,因為每次我們眨眼,世界都變換到我們腳下。每天每一刻每奈秒,世界都在變,電子互相碰撞,然後發生反應,人們互相碰撞,然後改變彼此的路徑,改變實屬不易,經常性的變化蜿蜒曲折,但或許這是好事,因為變化讓我們變得強大,讓我們具有韌性,令我們進化。
、 我們不禁會思考,一個人在這個世界上能起多大作用,我們自我審查、自我審問,我們有無做英雄或偉人的能耐?,但事實上,我們的一舉一動都會帶來影響,我們所做的每一件事,都影響我們身邊的人,我們所做的每一個選擇,都會為世界掀起漣漪,一個小小的善行,會為我們素昧平生的人,帶來一系列意料不到的益處,也許這些結果我們看不到,但它們確實發生了。萬事皆可能的一瞬間,我們做下決定或採取行動的那一刻,跨出第一步前所吸的一口氣,愛,引發了這些時刻、這些行動,這些決定,啟動了綿延長久的連鎖反應。
遞迴數列解法 在 吳老師教學部落格 Youtube 的精選貼文
Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境
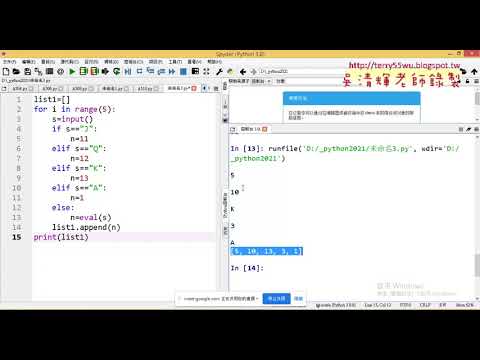
遞迴數列解法 在 吳老師教學部落格 Youtube 的精選貼文
Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境
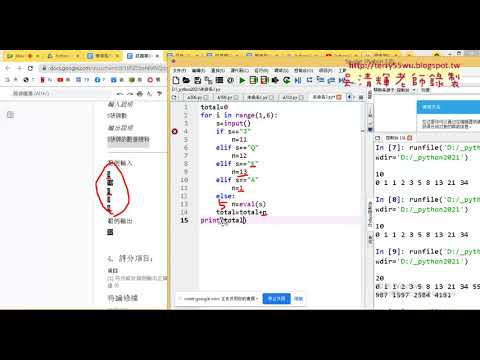
遞迴數列解法 在 吳老師教學部落格 Youtube 的最讚貼文
Python基礎程式語言應用證照班第10次上課
01_重點回顧與證照508最大公因數
02_證照508最大公因數解答
03_證照510費氏數列題目說明
04_證照510費氏數列無函式解答
05_證照510費氏數列加上函式解答
06_證照602撲克牌總和解答一
07_證照602撲克牌總和解答二改用串列
08_證照604眾數建立串列與新增
09_證照604眾數用COUNT計算次數
完整教學
http://goo.gl/aQTMFS
吳老師教學論壇
http://www.tqc.idv.tw/
教學論壇(之後課程會放論壇上課學員請自行加入):
https://groups.google.com/g/tcfst_python_2021_2
證照基礎程式語言 (Python 3)證照
Python 第1類:基本程式設計
技能內容:變數與常數、指定敘述、標準輸入輸出、運算式、算術運算子、數學函式的應用、格式化的輸出Python 第2類:選擇敘述
技能內容:if、if...else、if…elifPython 第3類:迴圈敘述
技能內容:while、for…inPython 第4類:進階控制流程
技能內容:常用的控制結構、條件判斷、迴圈Python 第5類:函式(Function)
技能內容:函式使用、傳遞參數、回傳資料、內建函式、區域變數與全域變數
上課用書:
Python 3.x 程式語言特訓教材(第二版)
作者: 蔡明志, 財團法人中華民國電腦技能基金會
出版社:全華
出版日期:2018/12/20
定價:490元
吳老師 110/9/14
EXCEL,VBA,Python,自強工業基金會,EXCEL,VBA,函數,程式設計,線上教學,PYTHON安裝環境

遞迴數列解法 在 高中數學討論區| 各位先進、各位同學們大家午安 ... 的推薦與評價
但在建中、南一中、嘉中等學校的考古題中都曾經出現過二階遞迴關係式的影子呦 🤩 ... 大家在「數列與級數」單元中必然有接觸到一階的遞迴關係式。 ... <看更多>
遞迴數列解法 在 混合型遞迴及其範例 - YouTube 線上影音下載 的推薦與評價
遞迴數列 速解 遞迴 英文筆型胰島素衛教 遞迴 好處二階 遞迴 平移成等比的 遞迴 胰島素混合型特殊 遞迴數列遞迴數列遞迴 java 遞迴 程式 數列 與 遞迴 關係公式 遞迴 排列組合 遞迴數列 速解 ... ... <看更多>





遞迴數列解法 在 [分享] 遞迴數列自創解法- 看板tutor - 批踢踢實業坊 的推薦與評價
沒想過要當補教名師
某天家教沒帶書忘了倍數遞迴怎麼解
卻反而偶然自創好用的新解法 某些情況(如公比為整數)解比較快
公比為分數一樣可以解
希望它有機會傳下去囉
或有人能幫我探索此解法的限制
例題: a(1)=4 a(n)=2/3 a(n-1)+5 求a(n)之通解?
1.原標準解法:
a(1)=4;a(2)= 23/3
a(2)-a(1) = 11/3
a(3)-a(2) = 2/3[a(2)-a(1)]
a(4)-a(3) = 2/3[a(3)-a(2)] = (2/3)^2[a(2)-a(1)]
a(5)-a(4) = 2/3[a(4)-a(3)] = (2/3)^3[a(2)-a(1)]
:
:
:
a(n)-a(n-1)= 2/3[a(n-1)-a(n-2)] = (2/3)^(n-2)[a(2)-a(1)]
___________________________________________________________
a(n)-a(1) = {1+2/3+(2/3)^2+(2/3)^3+……+(2/3)^(n-2)}x[a(2)-a(1)]
= {1[1-(2/3)^(n-1)]}/(1-2/3)x[a(2)-a(1)]
=> a(n) = 15 - 11(2/3)^(n-1)
2.妞式解法
a(1)=4 ; a(2)=23/3 ; a(3)=91/9
d(1)=a(2)-a(1)= 11/3
d(2)=a(3)-a(2)= 22/9
=>d(n)=11/3 x (2/3)^(n-1)
<以下重點>
令a(n) = Ad(n)+B
代入a(1)=4 = 11/3A + B
a(2)=23/3 = 22/9A + B
聯立解得 11/9 A = -11/3 =>A = -3
B = 15
代回a(n)解得 a(n) = 15-11 (2/3)^(n-1)
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 114.40.101.132
... <看更多>